Wissenbach, Moritz, University of Würzburg, Germany, moritz.wissenbach@uni-wuerzburg.de Pravida, Dietmar, University of Frankfurt, Germany, dpravida@goethehaus-frankfurt.de Middell, Gregor, University of Würzburg, Germany, gregor@middell.net
Introduction
Dating manuscripts is one of the most demanding tasks of textual scholarship (see e.g. Bockelkamp 1982; Tyson 1987). While there is a vast body of literature on dating and constituting witness stemmata for ancient and medieval codices (West 1973; Bischoff 2009), there seems to be hardly any systematic discussion on the issue of dating modern manuscripts. There have been successful approaches to date older material by computational phylogenetics (Robinson et al. 1998) with the consecutive import of quantitative methods and tools into the field, but to our knowledge, there is no approach that uses formal logics.1
Usually, the tools at the modern philologist’s disposal are very basic: A pencil or marker pen and a maximal writing surface (Figure 1: Reconstruction of the genesis of Faust manuscript VH2). In this paper, we examine the use of a formal knowledge representation to facilitate the dating of a large corpus of inscriptions on manuscripts. The knowledge representation is to be a
- point where diverse and possibly conflicting research sources can be integrated
- working tool for the philologist to be queried and modified during research
- basis of facts for a formal reasoning calculus
- database for users.
The quality of the results of automatic reasoning will be of special interest. Will they be incorrect or correct, and in case of the latter, will they be largely expected or to some degree unexpected?
Figure 1Relativedating of modern manuscripts
By inscription we understand any portion of written text on a manuscript in one specific phase of writing. If there is no absolute chronology at hand, the only possibility left is to try to give a relative chronology. We believe that a considerable part of conventional dating procedures can be reduced to a combination of more elementary steps that allow a more explicit and even formal approach.
Inductive vs. deductive reasoning
Relations between inscriptions can be used as predicates in a formal logic and reasoned upon by a suitable calculus. In order to reason deductively, a general rule or a set of rules is required. It is imaginable for this set to be induced automatically by a machine learning algorithm. In this study, however, the set of rules is manually defined. Thus, the presented approach is purely deductive.
Dealing with contradictions
Some assertions are taken from various sources of research, others are calculated automatically from existing data and even others are established manually. There will inevitably be contradictions. Possible solutions are:
- Do not try to resolve and thus conceal the contradictions.
- Try to specify explicit rules that prioritize one class of assertion over the other.
- Use a method of approximate reasoning.
We have decided for the second approach, as it preserves the advantages of the first while still enabling a very unambiguous specification and interpretation.
Reasoning rules for relative dating
To our knowledge there is no extensive list of typical modes of philological reasoning available, so we will try to give some elementary suggestions (following Pravida 2005:58f.).
Relations between inscriptions
Chronological anteriority
The relation that we are interested in as a result is a temporal one: Which inscriptions predate other inscriptions:
Syntagmatic precedence
Inscription I syntagmatically precedes a second inscription J if the text of J follows the text of I with respect to a larger text that contains them both:
Paradigmatic relationship
Inscription I is paradigmatically related to a second inscription J if they share text:
Text-genetic anteriority
Inscription I text-genetically precedes an inscription J, if I contains an earlier stage of a text contained by J:
Text-genetic anteriority by definition implies chronological anteriority.
Exclusive containment
The overall syntagmatic interval of one inscription, I, is said to be exclusively contained by the overall syntagmatic interval of another inscription J, if some part of the text of inscription I lies within the overall syntagmatic interval of inscription J, where they have a larger coherent textual neighbourhood than in inscription I:
The notion of exclusive containment captures the case of additional amplification of a passage. Exclusive containment is some special case of text-genetic posteriority with regard to some portion of an inscription. (Exclusive containment is very common in the working manuscripts of Brentano; we take it as a matter of course that it will be necessary to refine our set of relations as soon as we will extend our approach to other authors.)
Rules
Rules or axioms can be defined as a basis for deduction. The language we use is that of predicate logic. The transitivity of the predates relation, e.g., can be expressed as
Other properties of relations can be modelled for the respective relations accordingly.
Precedence
Rules that might potentially lead to contradictions need to be ordered, so that it is clear which rule has precedence over another. Consider the two rules
In order to subordinate rule b under rule a, we add a conjugation of the negated antecedent of the first rule:
In this way, all rules can be ordered and thus the set of rules be made logically consistent. In the following, we will list the rules ordered by priority from lowest to highest. The term pi is used to designate priority.
Syntagmatic precedence
Paradigmatic relations
The paradigmatic relation is symmetric. For dating, another hint (term c) must be considered (material, elementary genetic classification, textual):
Containment
Text-genetic anteriority
An Example from Clemens Brentano’s Romances of the Rosary
The twelfth canto of the Romances of the Rosary serves as an example that our default assumptions and their formalisation do in fact yield adequate results (cf. Pravida 2005; Brentano 2006). We consider the drafts (inscriptions) J1-6.
From the data which can be obtained from manuscript descriptions, we gather the relations shown in Figure 2:
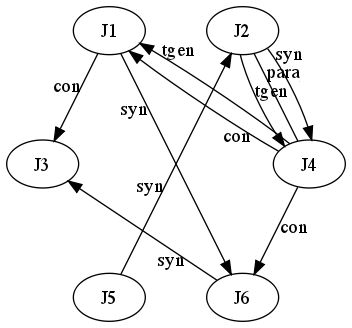
Figure 2
From textual evidence we know that:
(**)
Our reasoning machine concludes:
Which establishes a total order (Figure 3):
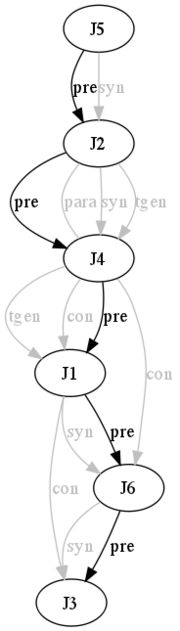
Figure 3
Application to the Faust edition / Outlook
The above example is well suited for our purpose, perhaps exceptionally so. Other texts may prove to be more difficult. Goethe’s habits of composing, for example, are much less linear. Yet, we can show that the genesis of the last act of Faust II can be captured in a way that resembles our example (Pravida, forthcoming). We expect that the genesis of the whole work will permit an analysis closely following these lines. As there is much more electronically encoded material, a computer-assisted approach seems very promising to us.
We used first-order logic and a theorem prover (Schulz 2002). The required expressivity of the logical formalism is probably lower than first-order logic (e.g. it will not need quantification), but more expressive than commonly used Semantic Web logics (e.g. OWL/SWRL) for the purpose of rule prioritisation. The adequacy of a non-monotonic logic, such as default reasoning (Reiter 1980; Delgrande & Schaub 1997), or multi-valued logics and approximate reasoning is to be evaluated. As many facts as possible should be automatically extracted or calculated from existing data, e.g. by means of automatic collation (Stolz & Dimpel 2006), etc.
References
Birdsall, J.N. (1992). The Recent History of New Testament Textual Criticism (from Westcott and Hort, 1881, to the present). In Aufstieg und Niedergang der römischen Welt. Geschichte und Kultur Roms im Spiegel der neueren Forschung. Vol. II,26,1. Berlin: de Gruyter, pp. 99-197.
Bischoff, B. (2009). Paläographie des römischen Altertums und des abendländischen Mittelalters. 4th ed. Berlin: Erich Schmidt.
Bockelkamp, M. (1982). Analytische Forschungen zu Handschriften des 19. Jahrhunderts. Hamburg: Hauswedell.
Brentano, C. (2006). Romanzen vom Rosenkranz. Frühe Fassungen. Ed. by Dietmar Pravida. Stuttgart: Kohlhammer 2006.
Delgrande, J. P., and T. Schaub (1997). Compiling Reasoning with and about Preferences into Default Logic. Proceedings of the International Joint Conference on Artificial Intelligence 1, pp. 168-175.
Greg, W. W. (1927). The Calculus of Variants. An Essay on Textual Criticism. Oxford: Clarendon.
Lachmann, C. (1842). Testamentum Novum Graece et Latine. Vol. 1. Berlin: Reimer.
Pravida, D. (2005). Die Erfindung des Rosenkranzes. Untersuchungen zu Clemens Brentanos Versepos. Frankfurt: Peter Lang.
Pravida, D. (forthcoming). Die Entstehung von Faust II, 5. Akt (1. Fassung). To appear in Jahrbuch des Freien Deutschen Hochstifts (2012)
Quentin, H. (1922). Mémoire sur l’établissement du texte de la Vulgate. 1re partie: Octateuque. Paris: Gabalda.
Reiter, R. (1980). A Logic for Default Reasoning. Artificial Intelligence 13: 81-132.
Robinson, P., A. Barbrook, N. Blake, and C. Howe (1998). The Phylogeny of ‘The Canterbury Tales’. Nature 394: 839-840.
Schulz, S. (2002). E – A Brainiac Theorem Prover. Journal of AI Communications 15(2/3): 111-126.
Stolz, M.. and F. M. Dimpel (2006). Computergestütztes Kollationieren und dynamische Textpräsentation – Ein Werkstattbericht aus dem Parzival-Projekt. http://nbn-resolving.de/urn:nbn:de:kobv:b4360-1004567
Tyson, A. (1987). Mozart: Studies of the autograph scores. Cambridge, Mass.: Harvard UP.
West, M. L. (1973). Textual criticism and editorial technique, applicable to Greek and Latin texts. Stuttgart: Teubner.
Notes
1.Our purpose of mechanizing the operation of manuscript dating has obvious parallels in various approaches (e.g. Quentin 1922; Greg 1927) of charting relationships between different manuscript readings by means of a formula system or a decision procedure (conveniently summarized in Birdsall 1992: 153sq). Dom Quentin, Greg and their followers could build on a highly sophisticated tradition of theoretical reflection on establishing manuscript genealogies without the intervention of subjective interpretation (Lachmann 1842: v) for which there is no analogue in our particular field of interest.
